Критерии оценки качества регрессионной модели, или какая модель хорошая, а какая лучше

В данной статье мы поговорим о том, как понять, качественную ли модель мы построили. Ведь именно качественная модель даст нам качественные прогнозы.

Инструмент «Моделирование и прогнозирование» Prognoz Platform обладает обширным списком моделей для построения и анализа. Каждая модель имеет свою специфику и применяется при различных предпосылках.

Объект «Модель» позволяет построить следующие регрессионные модели:

• Линейная регрессия (оценка методом наименьших квадратов);
• Линейная регрессия (оценка методом инструментальных переменных);
• Модель бинарного выбора (оценка методом максимального правдоподобия);
• Нелинейная регрессия (оценка нелинейным методом наименьших квадратов).

Начнём с модели линейной регрессии. Многое из сказанного будет распространяться и на другие виды.

Модель линейной регрессии (оценка МНК)

Под моделью линейной регрессии будем понимать модель вида:

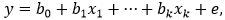
где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b₀, b₁, …, b_k – коэффициенты модели.

Итак, куда смотреть?

Коэффициенты модели

Для каждого коэффициента на панели «Идентифицированное уравнение» вычисляется ряд статистик:

• стандартная ошибка,
• t-статистика,
• вероятность значимости коэффициента.

Последняя является наиболее универсальной и показывает, с какой вероятностью удаление из модели фактора, соответствующего данному коэффициенту, не окажется значимым.

Открываем панель и смотрим на последний столбец, ведь он – именно тот, кто сразу же скажет нам о значимости коэффициентов.

Факторов с большой вероятностью незначимости в модели быть не должно.

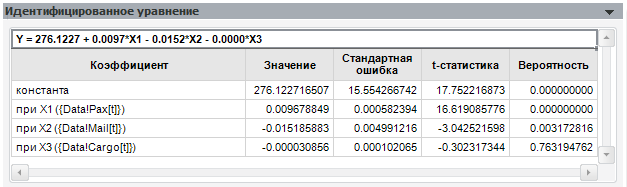
Как вы видите, при исключении последнего фактора коэффициенты модели практически не изменились.

Возможные проблемы: Что делать, если согласно вашей теоретической модели фактор с большой вероятностью незначимости обязательно должен быть? Существуют и другие способы определения значимости коэффициентов. Например, взгляните на матрицу корреляции факторов.

Матрица корреляции

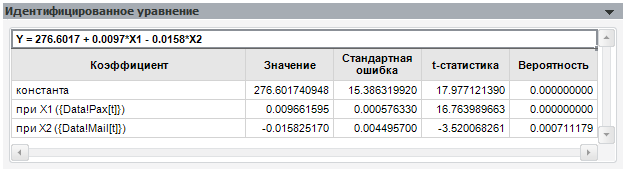
Панель «Корреляция факторов» содержит матрицу корреляции между всеми переменными модели, а также строит облако наблюдений для выделенной пары значений.

Коэффициент корреляции показывает силу линейной зависимости между двумя переменными. Он изменяется от -1 до 1. Близость к -1 говорит об отрицательной линейной зависимости, близость к 1 – о положительной.

Облако наблюдений позволяет визуально определить, похожа ли зависимость одной переменной от другой на линейную.

Если среди факторов встречаются сильно коррелирующие между собой, исключите один из них. При желании вместо модели обычной линейной регрессии вы можете построить модель с инструментальными переменными, включив в список инструментальных исключённые из-за корреляции факторы.

Матрица корреляции не имеет смысла для модели нелинейной регрессии, поскольку она показывает только силу линейной зависимости.

Критерии качества

Помимо проверки каждого коэффициента модели важно знать, насколько она хороша в целом. Для этого вычисляют статистики, расположенные на панели «Статистические характеристики».

Коэффициент детерминации (R²) – наиболее распространённая статистика для оценки качества модели. R² рассчитывается по следующей формуле: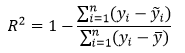

где:

n – число наблюдений;

y_i — значения объясняемой переменной;

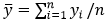— среднее значение объясняемой переменной;

ỹ_i — модельные значения, построенные по оцененным параметрам.

R² принимает значение от 0 до 1 и показывает долю объяснённой дисперсии объясняемого ряда. Чем ближе R² к 1, тем лучше модель, тем меньше доля необъяснённого.

Возможные проблемы: Проблемы с использованием R² заключаются в том, что его значение не уменьшается при добавлении в уравнение факторов, сколь плохи бы они ни были.

Он гарантированно будет равен 1, если мы добавим в модель столько факторов, сколько у нас наблюдений. Поэтому сравнивать модели с разным количеством факторов, используя R², не имеет смысла.

Для более адекватной оценки модели используется скорректированный коэффициент детерминации (Adj R²). Как видно из названия, этот показатель представляет собой скорректированную версию R², накладывая «штраф» за каждый добавленный фактор:

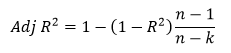
где k – число факторов, включенных в модель.

Коэффициент Adj R² также принимает значения от 0 до 1, но никогда не будет больше, чем значение R².

Аналогом t-статистики коэффициента является статистика Фишера (F-статистика). Однако если t-статистика проверяет гипотезу о незначимости одного коэффициента, то F-статистика проверяет гипотезу о том, что все факторы (кроме константы) являются незначимыми. Значение F-статистики также сравнивают с критическим, и для него мы также можем получить вероятность незначимости. Стоит понимать, что данный тест проверяет гипотезу о том, что все факторы одновременно являются незначимыми. Поэтому при наличии незначимых факторов модель в целом может быть значима.

Возможные проблемы: Большинство статистик строится для случая, когда модель включает в себя константу. Однако в Prognoz Platform мы имеем возможность убрать константу из списка оцениваемых коэффициентов. Стоит понимать, что такие манипуляции приводят к тому, что некоторые характеристики могут принимать недопустимые значения. Так, R² и Adj R² при отсутствии константы могут принимать отрицательные значения. В таком случае их уже не получится интерпретировать как долю, принимающую значение от 0 до 1.

Для моделей без константы в Prognoz Platform рассчитываются нецентрированные коэффициенты детерминации (R² и Adj R²). Модифицированная формула приводит их значения к диапазону от 0 до 1 даже в модели без константы.

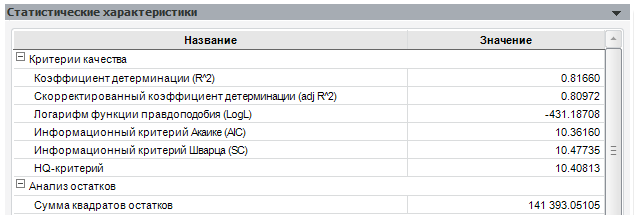
Посмотрим значения описанных критериев для приведённой выше модели:

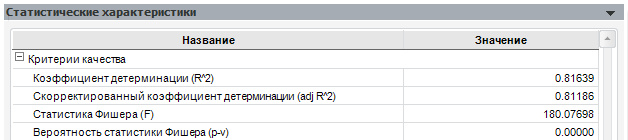
Как мы видим, коэффициент детерминации достаточно велик, однако есть ещё значительная доля необъяснённой дисперсии. Статистика Фишера говорит о том, что выбранная нами совокупность факторов является значимой.

Сравнительные критерии

Кроме критериев, позволяющих говорить о качестве модели самой по себе, существует ряд характеристик, позволяющих сравнивать модели друг с другом (при условии, что мы объясняем один и тот же ряд на одном и том же периоде).

Большинство моделей регрессии сводятся к задаче минимизации суммы квадратов остатков (sum of squared residuals, SSR). Таким образом, сравнивая модели по этому показателю, можно определить, какая из моделей лучше объяснила исследуемый ряд. Такой модели будет соответствовать наименьшее значение суммы квадратов остатков.

Возможные проблемы: Стоит заметить, что с ростом числа факторов данный показатель так же, как и R², будет стремиться к граничному значению (у SSR, очевидно, граничное значение 0).

Некоторые модели сводятся к максимизации логарифма функции максимального правдоподобия (LogL). Для модели линейной регрессии эти задачи приводят к одинаковому решению. На основе LogL строятся информационные критерии, часто используемые для решения задачи выбора как регрессионных моделей, так и моделей сглаживания:

• информационный критерий Акаике (Akaike Information criterion, AIC)
• критерий Шварца (Schwarz Criterion, SC)
• критерий Ханнана-Куина (Hannan-Quinn Criterion, HQ)

Все критерии учитывают число наблюдений и число параметров модели и отличаются друг от друга видом «функции штрафа» за число параметров. Для информационных критериев действует правило: наилучшая модель имеет наименьшее значение критерия.

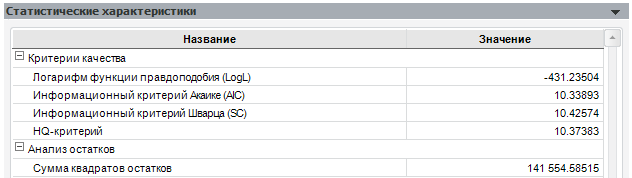
Сравним нашу модель с её первым вариантом (с «лишним» коэффициентом):

Как можно увидеть, данная модель хоть и дала меньшую сумму квадратов остатков, оказалась хуже по информационным критериям и по скорректированному коэффициенту детерминации.

Анализ остатков

Модель считается качественной, если остатки модели не коррелируют между собой. В противном случае имеет место постоянное однонаправленное воздействие на объясняемую переменную не учтённых в модели факторов. Это влияет на качество оценок модели, делая их неэффективными.

Для проверки остатков на автокорреляцию первого порядка (зависимость текущего значения от предыдущих) используется статистика Дарбина-Уотсона (DW). Её значение находится в промежутке от 0 до 4. В случае отсутствия автокорреляции DW близка к 2. Близость к 0 говорит о положительной автокорреляции, к 4 — об отрицательной.

Как оказалось, в нашей модели присутствует автокорреляция остатков. От автокорреляции можно избавиться, применив преобразование «Разность» к объясняемой переменной или воспользовавшись другим видом модели – моделью ARIMA или моделью ARMAX.

Возможные проблемы: Статистика Дарбина-Уотсона неприменима к моделям без константы, а также к моделям, которые в качестве факторов используют лагированные значения объясняемой переменной. В этих случаях статистика может показывать отсутствие автокорреляции при её наличии.

Модель линейной регрессии (метод инструментальных переменных)

Модель линейной регрессии с инструментальными переменными имеет вид:

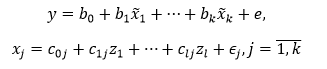
где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, x̃₁, …, x̃_k – смоделированные при помощи инструментальных переменных объясняющие ряды, z₁, …, z_l – инструментальные переменные, e, ∈_j – вектора ошибок моделей, b₀, b₁, …, b_k – коэффициенты модели, c_0j, c_1j, …, c_lj – коэффициенты моделей для объясняющих рядов.

Схема, по которой следует проверять качество модели, является схожей, только к критериям качества добавляется J-статистика – аналог F-статистики, учитывающий инструментальные переменные.

Модель бинарного выбора

Объясняемой переменной в модели бинарного выбора является величина, принимающая только два значения – 0 или 1.

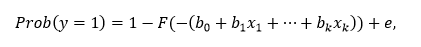
где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b₀, b₁, …, b_k – коэффициенты модели, F – неубывающая функция, возвращающая значения от 0 до 1.

Коэффициенты модели вычисляются методом, максимизирующим значение функции максимального правдоподобия. Для данной модели актуальными будут такие критерии качества, как:

• Коэффициент детерминации МакФаддена (McFadden R²) – аналог обычного R²;
• LR-статистика и её вероятность — аналог F-статистики;
• Сравнительные критерии: LogL, AIC, SC, HQ.

Нелинейная регрессия

Под моделью линейной регрессии будем понимать модель вида:

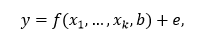
где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b – вектор коэффициентов модели.

Коэффициенты модели вычисляются методом, минимизирующим значение суммы квадратов остатков. Для данной модели будут актуальны те же критерии, что и для линейной регрессии, кроме проверки матрицы корреляций. Отметим ещё, что F-статистика будет проверять, является ли значимой модель в целом по сравнению с моделью y = b₀ + e, даже если в исходной модели у функции f (x₁, …, x_k,b) нет слагаемого, соответствующего константе.

Итоги

Подведём итоги и представим перечень проверяемых характеристик в виде таблицы:

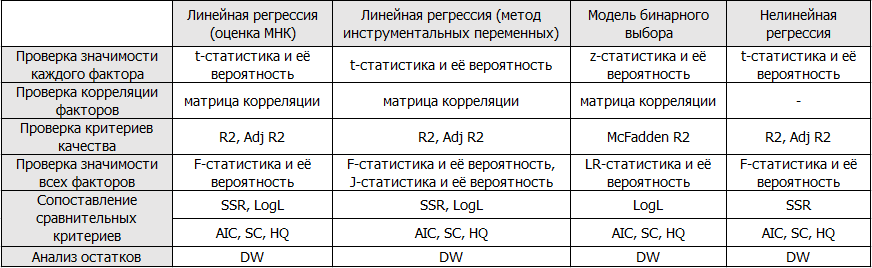
Надеюсь, данная статья была полезной для читателей!